Current research projects
Starting in September 2022, the focus of this BMBF funded AI junior research group “Multicriteria Machine Learning – Efficiency, Robustness, Inter-activity and System Knowledge” is on the development of multiobjective training algorithms for deep learning. Deep neural networks are of utmost importance in many areas of application. However, the consideration of multiple training criteria as well as system knowledge requires further investigation and has great potential for further improvements. In particular, we perform basic research on
- The development of efficient optimization algorithms for training neural networks regarding multiple conflicting objective functions
- Interactive learning and adaptation of deep neural networks using techniques from multiobjective optimization
- Consideration of system knowledge, e.g., in the form of conservation laws or differential equations
Click here for more information and the official press release.
Project: Hybrid Modeling for Data-enhanced Multiobjective Optimization of Multibody Systems
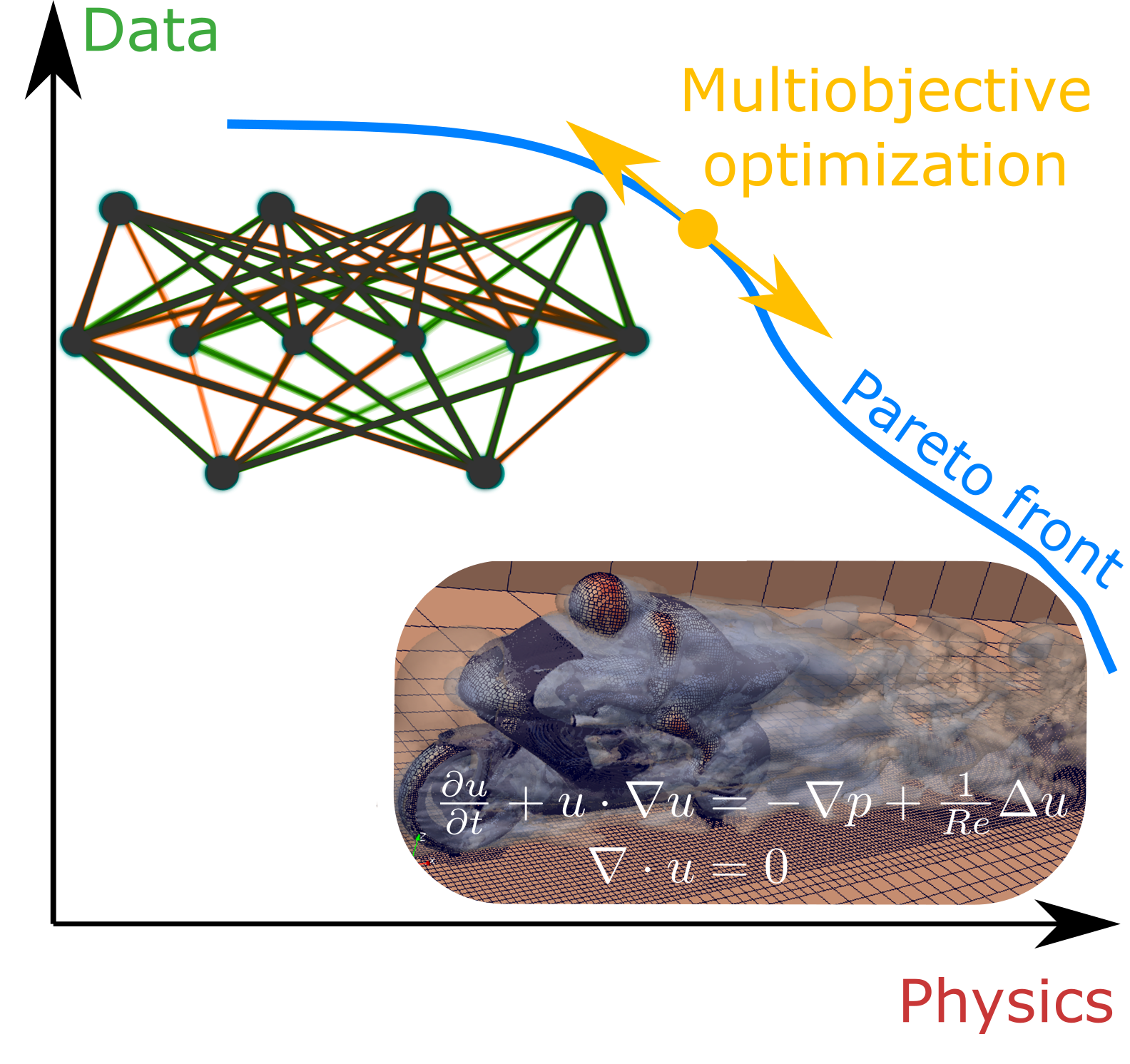
There is hardly ever a situation where only one goal is of interest at a time. When carrying out a purchase, for example, we want to pay a low price for a high quality product. In the same manner, multiple objectives are present in the design of essentially all technical systems such as fast and energy efficient electric vehicles, light yet stable constructions, or more generally the simultaneous achievement of technical, economic and ecological objectives. This dilemma leads to the field of multiobjective optimization, where the aim is to optimize all relevant criteria simultaneously. While one optimal solution is usually sufficient in the single-objective setting, there exists an infinite number of optimal compromises in the presence of multiple, contradictory objectives. Knowledge of the associated Pareto set allows for the well-informed selection of trade-off solutions and for the flexible adaptation of designs to changing prioritization or external influence factors.Conflicting criteria also occur in the design of complex multibody systems such as vehicle suspension systems, where the minimization of production costs and tire wear as well as the maximization of driving comfort and safety are highly desirable. The complexity of such multibody dynamics has been constantly increasing over the past years, the key enabler being the rapidly growing computational capabilities which allow for the simulation of increasingly detailed, large scale models. Despite the available computing resources, the multicriteria design of systems with such a high degree of complexity is still beyond today's computing powers.To address these challenges, the central goal of this research project is the development of a highly flexible and adaptive data-enhanced framework for the multicriteria design of complex multibody systems. The central components are the online collection of data from various sources, the data-driven and hybrid modeling (i.e., using equations and data at the same time) of individual components with varying degrees of accuracy, and the interactive multiobjective optimization of the resulting hybrid model. The intention behind the hybrid modeling is to exploit the best of both worlds, i.e., to use equations governing the physics where possible, and on the other hand to further enhance the performance and accuracy using data-driven models whenever the physics-based models are inaccurate, too expensive to evaluate, or even unknown.The developed methodology will be highly useful in the design of a large number of multibody systems, and will thus be of great use to other projects within the Priority Programme while at the same time contributing to the overall program goals.
Current systems that incorporate AI technology mainly target the introduction phase, where a core component is training and adaptation of AI models based on given example data. SAIL’s focus on the full life-cycle moves the current emphasis towards sustainable long-term development in real life. The joint project SAIL addresses both basic research in the field of AI, its implications from the perspective of the humanities and social sciences, and concrete applications in the field of Industry 4.0 and Intelligent Healthcare. SAIL is an interdisciplinary and interinstitutional collaboration of Bielefeld University, Paderborn University, Bielefeld University of Applied Sciences, and OWL University of Applied Sciences and Arts, funded by the MKW NRW.
Project headed by the DSE group: (Project R2.3) Human-centered continuous optimization
Manual workplaces involving both humans and technical machinery are usually optimized at design time. This ignores improvements due to human learning dur- ing long-term work. Therefore, we propose to study the application of Bayesian optimization and life-long learning with a human-centered focus, e.g., a suitable weighting of past and current data or a transfer between humans.
For more details, please refer to the website of the Joint Artificial Intelligence Institute (JAII).
In October 2021, a new research project was initialized under the title "DARE: Training, validation and benchmark tools for the development of data-driven operation and control strategies for intelligent, local energy systems" (German: "DARE: Trainings-, Validierungs- und Benchmarkwerkzeuge zur Entwicklung datengetriebener Betriebs- und Regelungsverfahren für intelligente, lokale Energiesysteme")
Within the next two years, researchers from the Software Innovation Campus Paderborn (SICP) and the Competence Centre for Sustainable Energy Technology (KET) will develop open source simulation and benchmark tools in collaboration with the industrial partners WestfalenWIND GmbH and Westfalen Weser Netz GmbH. The aim of the framework is to address challenges that may occur during the operation of decentralized energy grids, with the overarching goal to transform our current system of energy suppy towards a sustainable infrastructure that mainly consists of localized renewable energy sources.
Scientific partners:
- Dr.-Ing. Oliver Wallscheid (LEA)
- Jun.-Prof. Dr. Sebastian Peitz (DSE)
Official press release (in german): Link
In almost all technical applications, multiple criteria are of interest – both during development as well as operation. Examples are fast but energy efficient vehicles and constructions that have to be light as well as stable. The goal in the resulting multiobjective optimization problems is the computation of the set of optimal compromises – the so-called Pareto set. A decision maker can then select an appropriate solution from this set. In control applications, it is possible to quickly switch between different compromises as a reaction to changes in the external conditions.
The Pareto set generally consists of infinitely many compromise solutions, its numerical approximation is therefore considerably more expensive than the solution of scalar optimization problems. This can quickly result in prohibitively large computational cost, particularly in situations where solutions to the underlying system are computationally expensive. For instance, this is the case when the system is described by a partial differential equation (PDE). In this context, surrogate models that can be solved significantly faster than classical numerical approximations by the finite element method are frequently used. In the case of non-smooth PDEs, reducing the computational cost is particularly important since these problems are often significantly more expensive to solve than smooth problems. However, the surrogate models introduce an approximation error intro the system, which has to be quantified and considered both in the analysis and the development of numerical algorithms. For non-smooth problems, literature on this topic is currently scarce.
The goal of this project is the development of efficient numerical methods to solve multiobjective optimization problems that are constrained by non-smooth PDEs. In the first step, optimality conditions for the non-smooth PDE-constrained problems will be derived, and the (hierarchical) structure of the Pareto sets will be analyzed. Building on this, algorithms for the computation of Pareto sets will be developed for these problems. The methods will be used for the optimization of problems with max-terms, contact problems, and time dependent hybrid and switched systems. In order to handle the numerical effort, reduced order modeling techniques – such as Reduced Basis, Proper Orthogonal Decomposition, and more recent approaches based on the Koopman operator – will be extended to the non-smooth setting. This requires the consideration of inexactness in the convergence analysis. Finally, the algorithms will be applied to several different problem settings in cooperation with other members of the Priority Programme.
High-performance computing (HPC) has become an important method in many scientific fields, such as drug and climate research. However, the data centers with energy-intensive supercomputers release a lot of CO2. "Energy-optimized supercomputer networks through the use of wind energy" (ESN4NW): behind this title lies a new, nationwide collaborative project led by SICP - Software Innovation Campus Paderborn at the University of Paderborn. In cooperation with the SICP member company WestfalenWIND IT, the idea of developing a new HPC infrastructure with a sustainable concept was born. The German Federal Ministry of Education and Research (BMBF) is now funding the project for the next three years with around 2.5 million euros. The consortium also includes the University of Passau, the Fraunhofer Institute for Reliability and Microintegration IZM and the companies AixpertSoft GmbH, Rittal, Atos Deutschland and Zattoo.
Official press release (in german): Link
Anyone looking at the German climate balance cannot ignore the issue of railway transportation: Growth can only be CO2-neutral in the future if significantly more people and goods are transported by rail. Innovative technologies are required for rail transport to fully exploit its potential. This is exactly what the RailCampus OWL project is all about. Universities, railroads and industry are developing a unique innovation network for the rail technology of the future at the Minden site and are training students for the rail transport revolution. At a digital parliamentary evening on April 13, representatives from politics, business and science sealed the project with a memorandum of understanding.